Danjon Limit

From The Moon
Jump to: navigation, search

The Danjon Limit

(glossary entry)


Description

The Danjon Limit is French astronomer André Danjon's estimate of the smallest angular separation (center to center) between Sun and Moon at which a lunar crescent can be seen. Danjon set the value at about 7° based on the crescent observations available to him in the early 1930's. Despite the obvious difficulties of accurately interpreting a dim and slender Moon in a bright twilight sky, Danjon felt that the inability to detect crescents at smaller elongations was an intrinsic property of the Moon caused by the roughness of the lunar terrain preventing any direct sunlight striking the Moon's surface from being seen at smaller angles (even under the best of circumstances). More recent observations suggest, contrary to Danjon's conclusion, that this is mostly a perceptual problem, and that the sunlit crescent does not actually vanish (at least not at this angle).

Additional Information

Note: the author of this article has never seen the original articles by André Danjon, so the comments posted here are based almost entirely on the description of Danjon's work in the book by Ashbrook (1984). Danjon's diagrams (apparently copied from the Sky and Telescope articles) can also be seen in Figure 2 of Ilyas (1994).

For an idealized distant ball illuminated by a distant point source placed to one side, one always expects to see an illuminated crescent extending precisely half way (180°) around the periphery. This crescent is expected to grow systematically thinner as the angle between the ball and the light source gets less, but no change in length is expected. At least to visual observers on Earth, the crescent Moon viewed low in the twilight sky before sunrise or after sunset does not work quite this way. The length of a slender crescent (from tip to tip) appears distinctly less than 180°, and it appears systematically shorter on the days when it is the thinnest. André Danjon was probably not the first to notice this effect, but he seems to have been the first to investigate it systematically. Collecting numerous observations made at varying elongations (the angular separation between the centers of the Sun and Moon), he concluded that the length should shorten to zero -- that is, the crescent should vanish entirely -- whenever the elongation became less than about 7°.

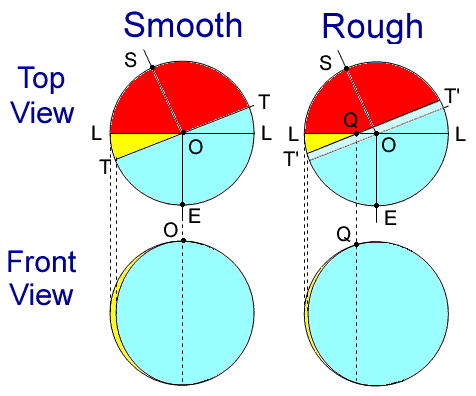
Danjon attributed this disappearance of the crescent to shadowing by the rugged lunar terrain. His reasoning can be explained by the following diagram adapted from Ashbrook (1984):

Danjon_Limit.GIF

The top views show a sphere as seen from above the plane containing the directions to the Sun (S) and Earth (E). If the sphere is smooth (left panel), the terminator line TT bounds the halves of the sphere bathed in sunlight and shadow; while the limb line LL bounds the halves visible and invisible from Earth. The wedge shaded in yellow is both in sunlight and visible from Earth; and, from Earth, it is seen as a full 180° crescent as shown in the frontal view. Its upper cusp is located at the point O. Danjon postulated that under the conditions that produce very thin crescents, the roughness of the Moon's surface produced additional shadowing that effectively moved the terminator line to some new position T’T’, encroaching on the previously sunlit side (as shown in the illustrations in right hand panel). As can be seen, this cuts into the yellow wedge, moving the upper cusp to a new position Q, which produces a less than 180° crescent, as is apparent in the frontal view.

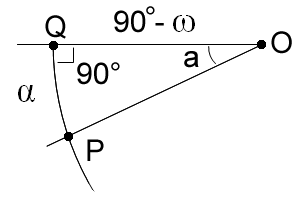
However, to explain the observational data the amount of displacement of the terminator had to vary with the phase. To quantify this variation Danjon drew the great circle line from E to Q, which crosses the original terminator line, TT, at some point P:

Danjon_Triangle.GIF

He called the distance from P to Q the deficiency of arc, symbolized by the Greek letter alpha: α (for thin crescents, this is essentially the same as the displacement of the terminator shown in the previous diagram). He also introduced the symbol ω (omega) for the angular half-length of the arc measured from the equator to the cusp position (ω = 90° for a full 180° crescent); and the symbol a for the elongation angle (which is the same as the twist between the directions TT and LL). Solving the resulting spherical triangle allowed Danjon to state a mathematical relationship between the three symbols:

    • Sin(α) = Sin(a) * Cos(ω)

>>
However as McNally (1983) pointed out, Danjon seems to have made an error in his math, for if this is the triangle he intended, the usual solution according to the rules of spherical trigonometry would give Tangents where he shows Sines. Schaefer (1991) explains this discrepancy by claiming it was Danjon's intention for the right angle to be at P instead of Q. Fortunately for the small angles involved the are nearly the same either way. Those familiar with trigonometry will see that α= 0 forces a full 180° crescent (ω= 90°) at all elongation angles; while the condition of α = a, if it should ever happen, forces the crescent length to zero.

Using his formula, Danjon was able to take his observed data (not all the observations were his own) for a and ω, and convert then to values of α; which in turn permitted him to make a plot of α (deficiency of arc) vs. a (elongation). His reason for doing this was that if the crescent length is plotted directly against elongation, the the rapid reduction of length to zero near the α = a limit produces a very unwieldy plot (see, for example, the one in Schaefer, 1991). By contrast, the parameter α changes very slowly.

Danjon's plot showed that a "normal" 180° crescent (zero deficiency of arc) is seen only at elongations around 40°. At larger elongations (rather wide crescents) the deficiency is actually negative, meaning that the arc is longer than 180° (try displacing the line T’T’ in the opposite direction from TT in the first diagram to see how this works). Below 40° a positive deficiency (arc less than 180°) was observed, and the amount of deficiency increased steadily. Although there were no observations at quite such small elongations, his plot made it appear one would have α = a (corresponding to zero crescent length) at around a= 7°, the value generally quoted as the Danjon Limit.

Discussion/Criticisms

It has never been entirely clear if the Danjon Limit is really an intrinsic property of the Moon (due to shadowing) as Danjon proposed; or if it merely a statement of the perceptual/psychological effects encountered in trying to visually detect a thin, dim target against a relatively bright background. It is also unclear if any experimental evidence has ever been collected to demonstrate if rough spheres actually act the way Danjon envisioned; and if so, what properties are needed to produce a behavior similar to the Moon. In addition, it is not entirely clear that modern reports, by observers with perhaps more dedication and experience than those upon Danjon had to rely, agree entirely with the older ones as to the shortness of thin crescents.
 
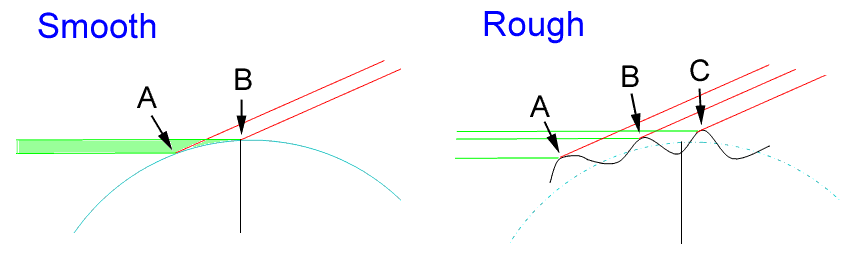
  The final diagram (not to scale, and not from Ashbrook or Danjon) explores whether it is logically plausible that the lunar topography could cause the central part of the crescent to be completely lost in shadow when the sun angle shining on the limb is 7°. The red lines represent the slanting lines of sunlight and the green lines are the lines of sight for an observer looking at the limb (nominally at the vertical black line) from Earth. To be visible from Earth as a sunlit feature, a surface element has to unblocked for both sets of lines.
 
 Danjon_Topography.GIF
 
  It the Moon were a smooth sphere, as shown on the left, the entire shaded swath between A and B would be seen in sunlight. Although the Moon as a whole is certainly not smooth, some areas (most notably the maria) might be fairly good approximation to this. From this diagram one might expect them to be visible at the limb even at zero elongation unless some fine scale surface roughness prevented this.
 
  The diagram on the right depicts an imaginary surface with a waviness that is steeper than the illumination angle of the sunlight. In this situation it seems plausible that the observed intensity would be greatly reduced, for most of the sunlit slopes would be hidden from view. However, unless they have infinitely sharp peaks, there should he small areas at the peaks of the ridges (in particular, at the points labeled A, B, and C) that are readily visible from Earth, yet where the surface is sloped in such a way that sunlight can strike it. If the basic waviness is reduced to where the maximum slopes are less steep than the illumination angle of the sunlight, then there would be broad areas visible from Earth with sunlight striking them (much as in the diagram on the left).
 
  In summary, it seems very hard to envision any reasonable topography that would give rise to a complete exclusion of sunlit areas visible from Earth, as Danjon seems to have proposed. If the surface undulations are less steep than the elongation angle, then the Moon would be expected to behave similarly to a smooth sphere. If the surface undulations are greater, the observed brightness will be greatly reduced by the hiding of much of the surface; however one would still expect that there would be isolated patches near the crests of the ridges where a frosting of light could be seen from Earth. The combination of foreshortening and grazing incidence would make these patches of light small and dim, but it is hard to see how they could be completely absent, unless this is caused by undulations on a finer scale.
 
  Finally, Martin Elsässer's recent image processing enhanced observations from mountain sites in the infrared have demonstrated that extensive areas of illumination are still visible from Earth at elongations as little as 4.7°, and observations from above the Earth's atmosphere have reportedly seen sun glints at the limb at elongations of as little as 2°. So it doesn't sound like the often quoted 7° Danjon Limit should be regarded as something intrinsic to the Moon with either a solid logical or observational basis.
 
  Despite all this, whether physically meaningful or not, Danjon's limit does appear to remain a useful description of the elongation at which visual sightings of the crescent Moon from Earth, low in a twilight sky, become extremely difficult. Indeed, Ilyas (1984), argues that the practical limit for most observers is closer to 10.5°.
 
  And it does seem that the appearance or disappearance of sunlit mountain slopes near the Moon's poles accounts for at least part of the lengthening and shortening of the crescent's cusps. Exactly how they change in appearance as the sun angle changes, and why we don't see them at certain phases (which seems somewhat unexpected from the above diagram), is probably a subject that needs more careful observational investigation.

LPOD Articles


More Observations of Thin Crescents

  • Reports (and often photos) of sightings of thin crescents can be found on the Islamic Crescents' Observation Project website and on the MoonWatch pages maintained by HM Nautical Almanac Office (UK).
  • French amateur Vincent Jacques has a collection of images of thin waxing and waning crescents close to conjunction, many (like those of Martin Elsässer) photographed in daytime using an infrared filter.


Bibliography


Retrieved from "http://the-moon.us/index.php?title=Danjon_Limit&oldid=10887"